Проверка работоспособности методики
Проверим вывод инвариантов подобия путем построения достаточного условия, например, на основании применения исчисления матрицы R по модулю простого числа. Для наличия в каждой строке матрицы C хотя бы одного ненулевого элемента достаточно, чтобы в каждой строке матрицы Cq , полученной из С путем вычисления остатка от деления соответствующего элемента на натуральное число q, существовал хотя бы один ненулевой элемент.
Действительно, пусть в i-й строке матрицы C все элементы равны нулю, тогда из определения матрицы Cq имеем
 |
21 |
Тогда достаточным условием вывода инвариантов подобия является требование, чтобы матрица C в системе уравнений размерности, построенной для него с учетом числовых констант и приведенной к виду, производя вычисления по модулю произвольного натурального числа q, не содержала нулевых строк.
Для корректного функционирования процесса необходимо, чтобы матрица C в системе уравнений размерности, приведенной к виду (4), не имела нулевых строк. Ранее было показано, что для выполнения этого условия достаточно, чтобы матрица Cq , полученная из матрицы C вычислением по модулю произвольного натурального числа q, не имела нулевых строк. Однако, в силу дистрибутивности операции вычисления остатка от деления на произвольно число q относительно операций сложения и умножения, применение исчисления по модулю q возможно уже на этапе приведения матрицы S к виду (4).
Данное условие является достаточным, но не необходимым. Действительно, при наличии в матрице Сq нулевых строк некоторые элементы в соответствующих строках в матрице С могут быть отличными от нуля, а именно - кратными q, а, следовательно, сам критерий может быть истинным. Приведенное условие преобразуется в необходимое, если поиск нулевых строк в матрице C производится для всех простых q. Более того, принимая во внимание диапазон исходных значений в матрице S и размерность матрицы S, возможно определить верхнюю границу списка простых чисел, достижение которой обеспечивает необходимость условия.
В общем случае трансформирование системы линейных уравнений по модулю простого числа имеет в три раза более высокую скорость исполнения. Это обусловлено отсутствием операций умножения рациональных чисел, каждая из которых содержит три операции умножения натуральных чисел (полагаем, что операции переноса и сложения имеют на порядок меньшую вычислительную трудоемкость по сравнению с операцией умножения). Исключение составляют исчисление по модулю 2 и по модулю 3.
Преобразование системы линейных уравнений по модулю 3 на множестве (-1, 0, +1) позволяет исключить из набора выполняемых операций умножение натуральных чисел. Все преобразования будут реализуемы с помощью сложения и арифметического отрицания. Это сокращает вычислительную трудоемкость проверки условия в несколько раз (в зависимости от параметров архитектуры ВС). Преобразование системы линейных уравнений по модулю 2 позволяет достичь еще большего быстродействия. Это достигается за счет возможности обрабатывать строки матрицы R как битовые последовательности, тем самым расходуя на сложение и перестановку строк по одной-двум командам микропроцессора. Перестановка столбцов при этом производится циклическими сдвигами двоичных значений.
Недостатками применения малых значений q при проверке необходимого условия является рост вероятности невыполнения условия при истинности значения критерия. Двумя величинами, критически влияющими на вероятность PFN в подобной ситуации, являются величина q и разность между количеством переменных и количеством условий, их связывающими (n-k). В первом приближении (без учета корреляции между значениями элементов матрицы R) данная зависимость описывается следующим выражением:
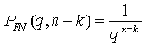 |
22 |
Поэтому предлагается:
либо проверить достаточное условие для q=3, что увеличивает скорость вычислений в (3·KMUL) раз при выполнении условия и незначительно (в (1+(1/(3·KMUL))) раз) замедляет скорость вычислений при невыполнении условия;
либо проверить условие для q=3 и для какого-либо простого q, большего трех, что увеличивает скорость вычислений примерно в 3 раза при выполнении условия и замедляет скорость вычислений в 1,33 раза при невыполнении условия.
(KMUL - коэффициент вычислительной трудоемкости операции целочисленного умножения по сравнению с операцией целочисленного сложения для данной аппаратной платформы).
Большее количество проверок с различными значениями q не приносит значимого увеличения средней скорости исчисления критерия. Выбор из предложенных вариантов производится на основе практических значений вероятности PFN и чаще всего обусловлен значением величины (n-k).
Выбор значения q, большего трех, для второго варианта проверки условия производится исходя из следующих соображений. Большие значения q более эффективны в связи с уменьшением вероятности PFN ложного невыполнения достаточного условия. Однако реализация линейных преобразований матрицы R по модулю q задействует предвычисления и хранение таблиц умножения и деления по модулю q, что требует определенных ресурсов вычислительной системы.
